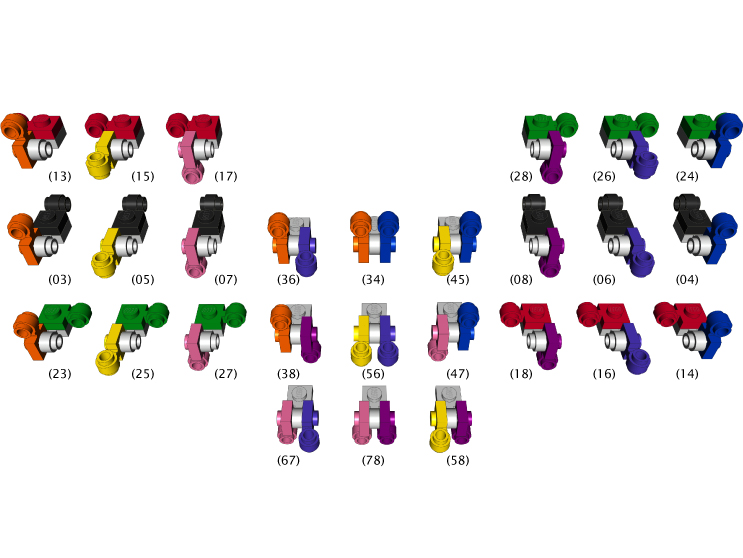
In point of fact, the possibility of “polyvalent” monomers is not going to be a practical consideration, yet, in terms of developing code. My first programming goal is to produce a recursive function that, given a base-9 number coding a clip-light polymer per my established notation for monovalent elements, will produce the corresponding LDraw file. Once that’s working, I will begin to embellish it with the capacity to handle bi- and tri-valent elements. But I wanted to go ahead enumerate the various polyvalent monomers and establish notation for them while I was thinking about it. Note that a parent monomer can bear no more than three children; we might say that a clip light with three children is “fully saturated.” Shown here are the “partially saturated” bi-valent monomers. There are twenty-seven of these. Note, also, the convention of ordering the digits indicating child monomers numerically: “32” is improper notation, while “23” is correct. I will follow the same convention in denoting the trivalent monomers, which will be enumerated in a subsequent post.

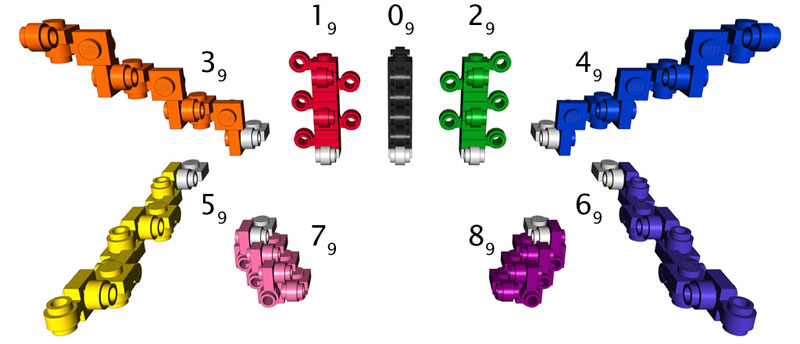
Subscripts indicate repeated monomer units, thus 0₉ = 000000000. Note that 7₉ and 8₉ are self-intersecting and closed.
More on the distinction between closed and open sequences later.

Fortunately, the well-known LDraw file standard provides a convenient platform for producing accurate renderings of complex Lego models. So we don’t have to physically build gigantic strings of clip lights to investigate their shapes and properties.

The image above was produced using LDView, an open-source real-time 3D viewer for LDraw model (.ldr) files, which came bundled with a distribution of Mike’s Lego CAD (MLCad) I downloaded some time ago. I think it probably still does.

The labels were added in Adobe Illustrator. They follow the standard notation I developed for indicating the relationship of a child monomer to its parent. Following the conventions of chemical empirical formulae, the subscripts indicate repeated monomer units, so that, for example 0₉ = 000000000. ¹ Remember that the starting monomer is never included in the notation string, so even though these are 10-mers, only 9 digits are required to describe them.

The .ldr files themselves were produced using a spreadsheet, as an exercise to understand the file format and the mathematics for calculating the position and rotation of a child monomer from those of its parent. A sample spreadsheet can be viewed here, and downloaded in OpenOffice format here.

In point of fact, this spreadsheet can be used to iterate any “bond” between two Lego elements indefinitely. For example, here’s a spiral made by stacking two elements 3822 (“Door 1 x 2 x 3 Left”), rotated 22.5° relative to each other, about the stud, and then iterating 19 more elements using the spreadsheet:

The remainder of this article will describe how the spreadsheet works.

Here’s an example .ldr file for the 5₉ model:

0 555555555             
0 Name: 555555555.ldr            
0 Author: MLCad            
0 Unofficial Model            
0 ROTATION CENTER 0 0 0 1 "Custom"       
0 ROTATION CONFIG 0 0          
1 7 0 0 0 1 0 0 0 1 0 0 0 1 4081B.DAT
1 14 -12 2 -20 0 1 0 -1 0 0 0 0 1 4081B.DAT
1 14 -10 14 -40 -1 0 0 0 -1 0 0 0 1 4081B.DAT
1 14 2 12 -60 0 -1 0 1 0 0 0 0 1 4081B.DAT
1 14 0 0 -80 1 0 0 0 1 0 0 0 1 4081B.DAT
1 14 -12 2 -100 0 1 0 -1 0 0 0 0 1 4081B.DAT
1 14 -10 14 -120 -1 0 0 0 -1 0 0 0 1 4081B.DAT
1 14 2 12 -140 0 -1 0 1 0 0 0 0 1 4081B.DAT
1 14 0 0 -160 1 0 0 0 1 0 0 0 1 4081B.DAT
1 14 -12 2 -180 0 1 0 -1 0 0 0 0 1 4081B.DAT
0

Per the .ldr file format specification, lines numbered 0 are comments or META commands, and can be ignored for illustrative purposes. Lines numbered 1 indicate the color, position, and rotation of a particular sub-file, in this case 4081B.DAT, which is the “Type 2” clip light part model. Simplifying further, let’s consider only the first two monomers in the chain:

1 7 0 0 0 1 0 0 0 1 0 0 0 1 4081B.DAT
1 14 -12 2 -20 0 1 0 -1 0 0 0 0 1 4081B.DAT

The second number on each line indicates the part’s color code. Per my convention, the starting monomer is always colored gray (7), and a child monomer in a “5” bond with its parent is always colored yellow (14). Stripping out the line numbers and color codes, and adding some spaces so everything lines up purty, gives:

  0   0   0  1  0  0  0  1  0  0  0  1  4081B.DAT
-12   2 -20  0  1  0 -1  0  0  0  0  1  4081B.DAT

Finally, since the part file is always going to be the same (for now), we can strip those off the ends:

  0   0   0  1  0  0  0  1  0  0  0  1
-12   2 -20  0  1  0 -1  0  0  0  0  1

Now we’re down to the heart of the matter. The first three numbers on each line are an ordered triple indicating the part’s x, y, z position in space. The remaining nine are the columns of a 3×3 matrix that describes its rotation.

The starting monomer is set at the origin (0, 0, 0), and its rotation matrix to the 3×3 identity matrix:

In MLCad, this can be done by opening a new model, inserting a part, and then right-clicking on it and selecting “Enter Pos.+Rot….” The first child monomer is then “manually” attached to the starting monomer, in the correct position and rotation, using MLCad’s graphical interface. Its position and rotation can then be read out of the saved .ldr file or the GUI dialog.

Determining the position of third and subsequent monomers in the chain, based on the first two elements, requires calculating the x, y, z position and the rotation matrix. If the starting element is at 0, 0, 0 and has the identity rotation matrix, then the x, y, z position of the second monomer can be thought of as the characteristic displacement of the iteration, and the rotation matrix of the second monomer can be described as the characteristic rotation of the iteration.

To calculate the position x’, y’ ,z’ of subsequent monomers, we apply the characteristic displacement and rotation values for the iteration to the x, y, z position of the parent monomer. Put differently, no matter how many links down the chain we may be, we will always use the position and rotation values of the second monomer in the chain to determine the position of any child monomer. And we do it with this formula

x’ = ax + by + cz + X
y’ = dx + ey + fz + Y
z’ = gx + hy + iz + Z

where X, Y, Z is the characteristic displacement (-12, 2, -20 in this case) and the characteristic rotation matrix is

Plugging in all the values gives

x’ = ax + by + cz + X = -12(0) + 2(1) + (-20)(0) + (-12) = -10
y’ = dx + ey + fz + Y = -12(-1) + 2(0) + (-20)(0) + 2 = 14
z’ = gx + hy + iz + Z = -12(0) + 2(0) + (-20)(1) + (-20) = -40

which is the position of the third monomer. Again, the important thing to note is that, to determine the position of the fourth and subsequent elements, we will use exactly the same values of a, b, c, d, e, f, g, h, u, X, Y, and Z that we just used. The only values that will change are x, y, and z, which will be the x, y, and z, position values of whatever parent element we’re working with.

Determining the rotation matrix of the third and subsequent elements requires matrix multiplication. Instruction in the details of matrix multiplication is beyond the scope of this article, but there are plenty of tutorials available around the tubes. Wikipedia is usually a good place to start. Assuming you understand matrix multiplication, determining the rotation matrix of subsequent monomers is simple: all you do is multiply the parent monomer’s rotation matrix by the characteristic rotation matrix, which has the same values of a, b, c, d, e, f, g, h, and i that were used immediately above.

Next up: writing a basic PERL function that accepts position and rotation information of a parent element, as well as a single digit 0-8 indicating the bonding relationship of the child monomer, and returns correct color, position, and rotation information for the child monomer in .ldr format.

Anyone who tinkers much with Lego soon develops an affection for element 4081—the so-called “clip light.” ¹ It consists of a 1×1 square plate with a vertical, circular “clip” attached to one side. This “clip” is unique, to my knowledge, among Lego elements, in that it consists, essentially, of a plate with studs on both sides.

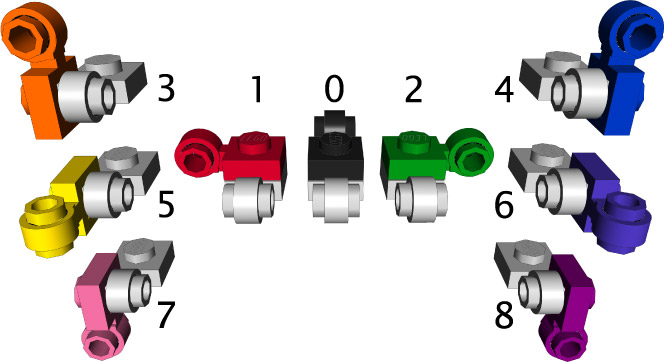
I am interested in the many ways that long “polymers” of clip lights can be strung together, and the shapes that result. The metaphor to polymer chemistry is very useful, and I will be using its terms pretty freely. The “monomer,” then, in all cases, is a single clip light element. And to understand the properties of the polymers, we need to first consider the set of possible “dimers”—that is, all the ways that one clip light can “bond” to another.

There are nine of them, that I have identified, and I have numbered them 0-8 and color-coded them according to the diagram above. To identify a particular bond, we first rotate the parent monomer into “standard position,” indicated above by the recurring gray monomer, which is, as presented, with the stud on top and the edge bearing the clip rotated toward the viewer. The nine orientations in which a child monomer can bond to the parent are then enumerated. The color of any monomer is determined by its relationship to its parent monomer. The starting monomer, which has no parent, is always colored gray.

Even numbers are given “cool” colors and correspond to “right-handed” bonds, while the corresponding “left-handed” bonds are given odd numbers and “warm” colors. Black, a neutral color, is reserved for the only non-enantiogenic bond relationship, the plate-to-plate back-to-back bond, and is numbered 0.